HOT100：二叉树

33 二叉树的中序遍历

中序遍历是先左子树，再根节点，最后是右节点的顺序。递归的写法比较直观：

List<Integer> ans = new ArrayList<>();

public List<Integer> inorderTraversal(TreeNode root) {
    dfs(root);
    return ans;
}

public void dfs(TreeNode root){
    if (root == null){
        return;
    }
    dfs(root.left);     // 先遍历左子树
    ans.add(root.val);  // 保存根节点的值
    dfs(root.right);    // 再遍历右子树
}

迭代的版本就是使用一个栈，模拟递归的过程：

public List<Integer> inorderTraversal(TreeNode root) {
    List<Integer> ans = new ArrayList<>();
    Deque<TreeNode> st = new ArrayDeque<>();

    while (root != null || !st.isEmpty()){
        // 先一直遍历左子树
        while (root != null){
            st.push(root);
            root = root.left;
        }
        // 左子树遍历结束，保存根节点的值
        root = st.pop();
        ans.add(root.val);
        // 切换到右子树继续遍历
        root = root.right;
    }
    return ans;
}

34 二叉树的最大深度

根节点的深度为 0，其他节点的深度是左右子树的最大深度 + 1。

public int maxDepth(TreeNode root) {
    if (root == null){
        return 0;
    }
    int l = maxDepth(root.left);
    int r = maxDepth(root.right);
    return Math.max(l, r) + 1;
}

35 翻转二叉树

public TreeNode invertTree(TreeNode root) {
    // 空节点不用翻转
    if (root == null){
        return root;
    }
    // 翻转左子树
    TreeNode left = invertTree(root.left);
    // 翻转右子树
    TreeNode right = invertTree(root.right);
    // 翻转当前节点
    root.left = right;
    root.right = left;
    return root;
}

36 对称二叉树

除去根节点的两颗左右子树是对称二叉树的关键信息在于：

• 两颗子树的根节点相同；

• 一棵树的左子树和另一颗数树右子树相同；

• 一棵树的右子树和另一颗数树左子树相同。

public boolean isSameTree(TreeNode p, TreeNode q) {
    if (p == null || q == null){
        return p == q;
    }
    return p.val == q.val && isSameTree(p.left, q.left) && isSameTree(p.right, q.right);
}

37 二叉树的直径

int ans = 0;

public int diameterOfBinaryTree(TreeNode root) {
    dfs(root);
    return ans;
}

public int dfs(TreeNode root){
    // 叶子节点链长为 0，空节点链长为 -1
    if (root == null){
        return -1;
    }
    int l = dfs(root.left) + 1;     // 左子树最大链长
    int r = dfs(root.right) + 1;    // 右子树最大链长
    ans = Math.max(ans, l + r);     // 两链拼成路径
    return Math.max(l, r);          // 当前子树最大链长
}

38 二叉树的层序遍历

使用队列（Queue）按层遍历二叉树。

public List<List<Integer>> levelOrder(TreeNode root) {
    List<List<Integer>> ans = new ArrayList<>();
    if (root == null){
        return ans;
    }
    // 创建队列，插入根节点
    Deque<TreeNode> q = new ArrayDeque<>();
    q.offer(root);

    while(!q.isEmpty()){
        // 按层遍历
        int n = q.size();
        List<Integer> layer = new ArrayList<>();
        for (int i = 0; i < n; i++){
            TreeNode node = q.poll();
            layer.add(node.val);
            if (node.left != null) q.offer(node.left);
            if (node.right != null) q.offer(node.right);
        }
        ans.add(layer);
    }
    return ans;
}

39 将有序数组转换为二叉搜索树

public TreeNode sortedArrayToBST(int[] nums) {
    return dfs(nums, 0, nums.length);
}

// 把 [left, right - 1] 转换成二叉搜索树
private TreeNode dfs(int[] nums, int left, int right){
    if (left == right){
        return null;
    }
    int m = left + (right - left) / 2;
    return new TreeNode(nums[m], dfs(nums, left, m), dfs(nums, m + 1, right));
}

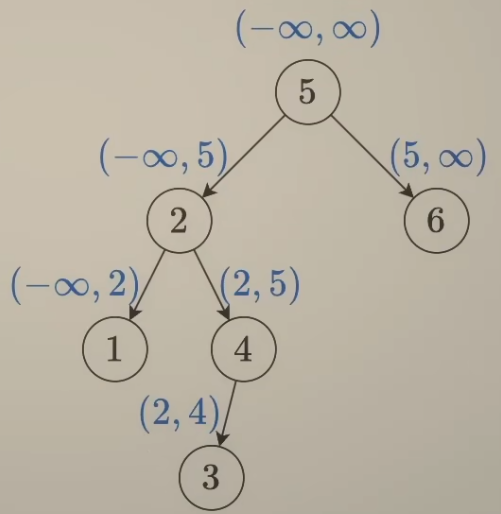
40 验证二叉搜索树 ⭐

通过数值的区间范围来验证二叉搜索树。

public boolean isValidBST(TreeNode root) {
    return isValidBST(root, Long.MIN_VALUE, Long.MAX_VALUE);
}

public boolean isValidBST(TreeNode root, long left, long right) {
    if (root == null) {
        return true;
    }
    int x = root.val;
    return left < x && x < right &&
            isValidBST(root.left, left, x) &&
            isValidBST(root.right, x, right);
}

41 二叉搜索树中第 K 小的元素 ⭐

二叉搜索树的中序遍历就是从小到大遍历的，中序遍历过程中第 k 个出现的元素就是答案。

int k;
int ans;

public int kthSmallest(TreeNode root, int k) {
    this.k = k;
    dfs(root);
    return ans;
}

public void dfs(TreeNode root){
    if (root == null || k == 0){
        return;
    }
    dfs(root.left);
    if (--k == 0){
        ans = root.val;
    }
    dfs(root.right);
}

42 二叉树的右视图

使用层序遍历，将每一层的最后一个元素加入答案即可。

public List<Integer> rightSideView(TreeNode root) {
    List<Integer> ans = new ArrayList<>();
    if (root == null){
        return ans;
    }
    Deque<TreeNode> q = new ArrayDeque<>();
    q.offer(root);

    while (!q.isEmpty()){
        int n = q.size();
        for (int i = 0; i < n; i ++){
            TreeNode node = q.poll();
            // 最右侧元素，加入答案
            if (i == n - 1){
                ans.add(node.val);
            }
            if (node.left != null) q.offer(node.left);
            if (node.right != null) q.offer(node.right);
        }
    }

    return ans;
}

本题也可以使用 DFS 解决，具体思路：先递归右子树，再递归左子树，当某个深度首次到达时，对应的节点就在右视图中。

public List<Integer> rightSideView(TreeNode root) {
    List<Integer> ans = new ArrayList<>();
    dfs(root, ans, 0);
    return ans;
}

public void dfs(TreeNode root, List<Integer> ans, int depth) {
    if (root == null){
        return;
    }
    // 首次到达某个深度
    if (ans.size() == depth){
        ans.add(root.val);
    }
    dfs(root.right, ans, depth + 1);
    dfs(root.left, ans, depth + 1);
}

43 二叉树展开为链表

头插法，从最后一个节点开始，依次向前插入节点。因此需要「右子树-左子树-根节点」的顺序 DFS 遍历树。

TreeNode head;

public void flatten(TreeNode root) {
    if (root == null){
        return;
    }
    flatten(root.right);
    flatten(root.left);
    root.left = null;
    root.right = head;
    head = root;
}

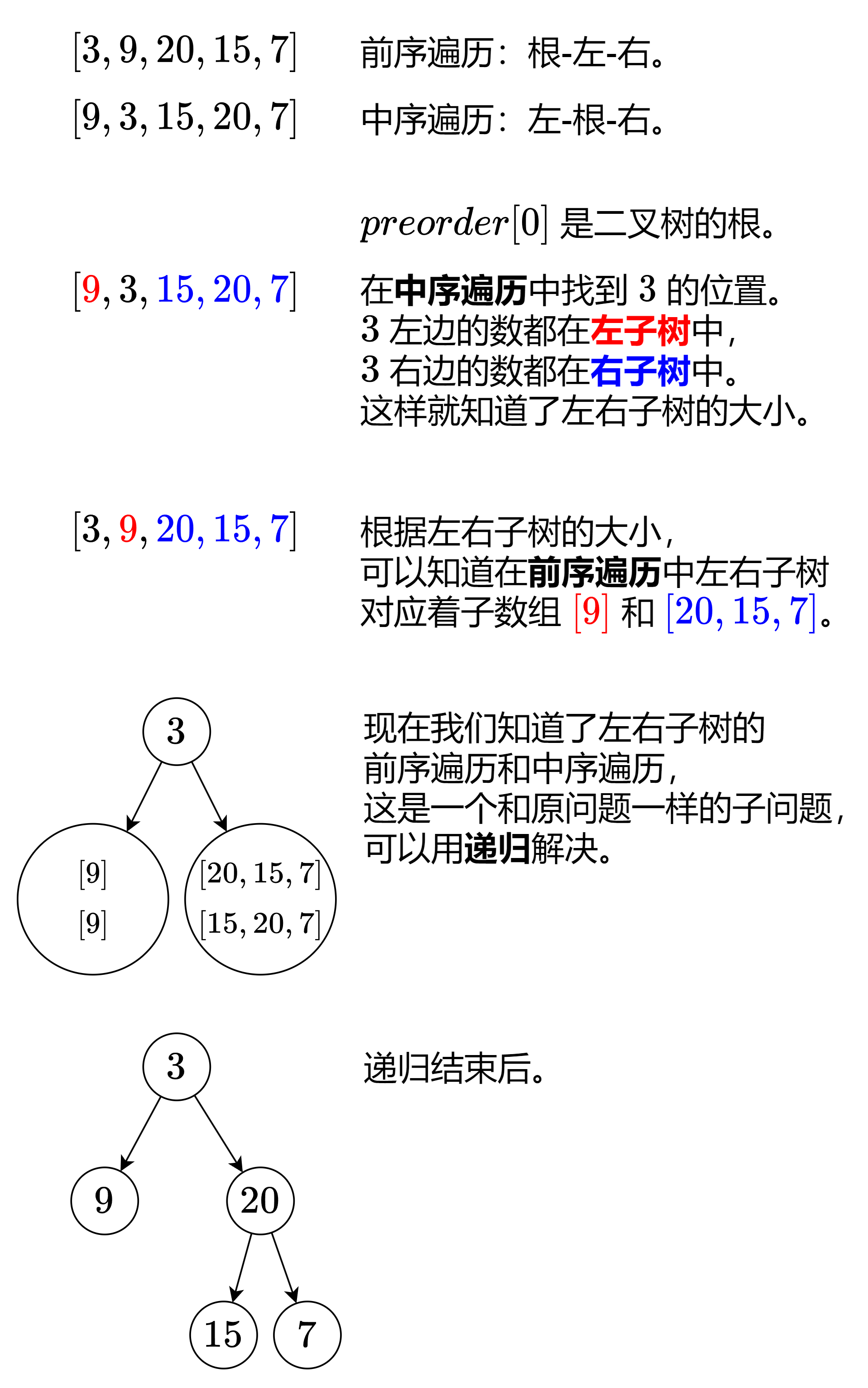
44 从前序与中序遍历序列构造二叉树 ⭐

public TreeNode buildTree(int[] preorder, int[] inorder) {
    // 中，左，右
    // 左，中，右
    int n = preorder.length;
    if (n == 0){
        return null;
    }
    // 左子树的大小
    int leftSize = indexOf(inorder, preorder[0]);

    int[] preL = Arrays.copyOfRange(preorder, 1, 1 + leftSize);
    int[] preR = Arrays.copyOfRange(preorder, 1 + leftSize, n);
    int[] inL = Arrays.copyOfRange(inorder, 0, leftSize);
    int[] inR = Arrays.copyOfRange(inorder, leftSize + 1, n);

    TreeNode left = buildTree(preL, inL);
    TreeNode right = buildTree(preR, inR);

    return new TreeNode(preorder[0], left, right);
}

public int indexOf(int[] a, int x){
    for (int i = 0; ; i++){
        if (a[i] == x){
            return i;
        }
    }
}

45 路径总和 III

int ans;
int targetSum;
Map<Long, Integer> cnt = new HashMap<>();

public int pathSum(TreeNode root, int targetSum) {
    cnt.put(0L, 1);
    this.targetSum = targetSum;
    return dfs(root, 0);
}

public int dfs(TreeNode root, long sum) {
    if (root == null) {
        return 0;
    }
    sum += root.val;
    int res = cnt.getOrDefault(sum - targetSum, 0);
    cnt.merge(sum, 1, Integer::sum);
    res += dfs(root.left, sum);
    res += dfs(root.right, sum);
    cnt.merge(sum, -1, Integer::sum); // 恢复现场
    return res;
}

46 二叉树的最近公共祖先

public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
    if (root == null || root == p || root == q){
        return root;
    }
    TreeNode left = lowestCommonAncestor(root.left, p, q);
    TreeNode right = lowestCommonAncestor(root.right, p, q);
    if (left != null && right != null){
        return root;
    }
    return left != null ? left : right;
}

47 二叉树中的最大路径和

int ans = Integer.MIN_VALUE;

public int maxPathSum(TreeNode root) {
    dfs(root);
    return ans;
}

public int dfs(TreeNode root){
    if (root == null){
        return 0;
    }
    int leftVal = dfs(root.left);
    int rightVal = dfs(root.right);
    ans = Math.max(ans, leftVal + rightVal + root.val);
    return Math.max(Math.max(leftVal, rightVal) + root.val, 0);
}

参考

部分思路参考了力扣官方题解和灵茶山艾府题解。